Voltar para a Biblioteca Romer
Bizonyos bizonytalanságok: A matematika a mikotoxin minőségellenőrzési anyagok mögött és hogyan kell használni azt
Publicado em:
Mikotoxin

Szervizlaboratóriumi körülmények között általában ugyanolyan körülmények között elemzik őket, mint amilyen körülmények között az ügyfélmintákat elemzik. A QCM-ek elemzése olyan adatokat hozhat létre, amelyeket a laboratóriumok felhasználhatnak egy újonnan kifejlesztett módszer teljesítményének ellenőrzésére, az elemzéssel kapcsolatos esetleges problémák elhárítására és minőségellenőrzési diagramok készítésére.
A mérési eljárások validálása során az elemzők a QCM egyes mérései által generált értéket a tanúsítványban feltüntetett hitelesített értékkel hasonlítják össze. Nem hivatalosan egyesek ezt az összehasonlítást kvalitatív módon írják le olyan kijelentésekkel, mint például: "a mért érték jól egyezik a minőségellenőrzési anyag tanúsított értékével". A kvantitatív megközelítés azonban matematikailag is össze tudja hasonlítani ezt a két értéket, ezáltal kizárva a torzítást, és eszközt biztosítva az eredmények időbeli nyomon követésére.
Ebben a cikkben Martina Bellasio végigvezeti Önt a bizonytalanságmérés számításának alapjain és azon, hogyan lehet számszerűsíteni azt a QCM-ekben.
Miért előnyösebb a kvantitatív megközelítés a QCM-ekben a bizonytalanság mérése során?
A kvantitatív megközelítés figyelembe veszi a gyakorlati alkalmazás során mért értéket, a QCM gyártója által hitelesített értéket és a hozzájuk tartozó bizonytalanságokat. Először röviden tárgyaljuk meg a mérési bizonytalanság fogalmát, és azt, hogy miért fontos figyelembe venni azt.
Minden mérés bizonytalansággal jár: egyetlen mérés sem pontos. Ezért a bizonytalanság kulcsfontosságú tényező a tudományos adatok értelmezésében, mivel információt ad arról, hogy a hozzárendelt értéket mennyire tartjuk pontosnak. Az értékhez kapcsolódó bizonytalanság számszerűsítésével teljesebb képet lehet adni az eredményekről, így azok hasznosabbá válnak. Az "ISO Guide to the Expression of Uncertainty in Measurement (GUM)" és az Eurachem/CITAC "Quantifying Uncertainty in Analytical Measurement" című útmutatója a bizonytalanság kifejezésére vonatkozó, gyakran használt referenciaszövegek.
Mint korábban említettük, a mért érték(ek) összehasonlítása egy minőségi ellenőrző anyag hitelesített értékével megköveteli e két érték közötti különbség és az úgynevezett kiterjesztett bizonytalanság kiszámítását. A következő bekezdésekben megtanuljuk, hogyan kell kiszámítani ezeket az értékeket, és hogyan kell alkalmazni őket egy gyakorlati példában.
Publicado em:
Mikotoxin
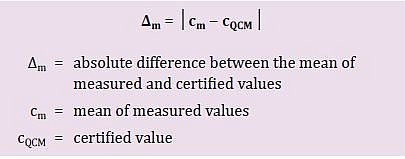
Hogyan határozható meg, hogy a mért érték milyen mértékben tér el a hitelesített értéktől?
1. lépés: Határozza meg a hitelesített érték és a mért értékek átlaga közötti különbséget (∆m).
Ebben a lépésben kiszámítjuk a hitelesített érték és a mért értékek átlaga közötti abszolút különbséget (∆m szimbólummal jelölve) (1. képlet). Itt a mért értékek átlagát vesszük, mivel az eredmény pontosságának garantálása érdekében minden mintát többször kell megmérni.
lépés: Számítsuk ki a kombinált bizonytalanságot (u∆).
Most kiszámítjuk a kombinált bizonytalanságot (u∆) (2. képlet). Ehhez a hitelesített érték és a mért értékek egyedi bizonytalanságait (lásd alább) már ismerni kell (lásd "Az egyedi bizonytalanságok meghatározása" című keretes írást). A 2. képlet mutatja a pontos matematikai műveleteket.
lépés: Számítsa ki a kiterjesztett bizonytalanságot (U∆).
Itt a kombinált bizonytalanságot megszorozzuk egy lefedettségi tényezővel, amely általában 2-vel egyenlő.
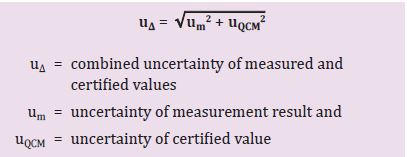
lépés: Hasonlítsa össze a hitelesített érték és a mért értékek közötti különbséget (∆m) a kiterjesztett bizonytalansággal (U∆).
A mért értékek és a hitelesített érték átlaga közötti abszolút különbség (Δm) és a kiterjesztett bizonytalanság (U∆) a két fő paraméter annak meghatározásában, hogy a mért érték jelentősen eltér-e a hitelesített értéktől. A "jelentős eltérést" így határozzuk meg: ha Δm kisebb vagy egyenlő, mint U∆, akkor nincs jelentős eltérés a mérési eredmény és a hitelesített érték között.
A mért értékek átlaga és a hitelesített érték abszolút különbségének összehasonlítása a kiterjesztett bizonytalansággal lehetővé teszi a két érték összehasonlításának matematikai megközelítését, és a laboratóriumokat az ISO 98-3:2008 útmutatónak (ISO Guide to the Expression of Uncertainty in Measurement, GUM) megfelelően tartja.
Bár a mérési bizonytalanság fogalma első pillantásra kissé nehezen érthető, egy mérési eljárás pontosságának másokhoz viszonyított mértékére vonatkozó kijelentésként szolgálhat. Ennek a bizonytalanságnak a számszerűsítése nagyban hozzájárul annak biztosításához, hogy megbízhatunk módszereinkben, és objektívebb és kevésbé a kvalitatív kijelentésekre támaszkodó eredményeket produkálhatunk: ahelyett, hogy például azt állítanánk, hogy "a mért érték megegyezik a hitelesített értékkel", a bizonytalanság kiszámítása lehetővé teszi számunkra, hogy az eltéréseket nagyobb és nagyobb pontossággal, és jobban alkalmazható módon ábrázoljuk és dokumentáljuk. A minőségellenőrzési anyagokkal a laboratóriumok egy hatékony eszközzel rendelkeznek, amely segíthet nekik módszereik folyamatos javításában.
Az alábbiakban egy példa segít megvilágítani ezeket az elveket.
Megjegyzés: A szöveg nagy része Thomas Linsinger "Egy mérési eredmény összehasonlítása a hitelesített értékkel" című ERM alkalmazási jegyzetéből származik.

Példa
Egy QCM-hez 12,9 µg/kg aflatoxin érték van rendelve, ± 0,9 µg/kg U becsült kiterjesztett bizonytalansággal és k = 2 lefedettségi tényezővel. Az UQCM, a tanúsított érték bizonytalansága úgy számítható ki, hogy az UQCM-et elosztjuk a lefedettségi tényezővel, így uQCM = 0,9/2 μg/kg= 0,45 μg/kg.
12 laboratóriumi mérést végeztek, amelyek átlagosan 14,3 ± 1,8 μg/kg értéket adtak. A mért értékek bizonytalanságát (um) ebben az esetben a szórás segítségével becsüljük meg. A szórást elosztjuk a mérések számának négyzetgyökével. um durván 1,8/√6 μg/kg = 0,74 μg/kg.
Mivel mind a hitelesített érték bizonytalansága, mind a mérés bizonytalansága a kezünkben van, most már ki tudjuk értékelni, hogy van-e jelentős különbség a mért és a hitelesített érték között.
Először is, a mért értékek és a hitelesített érték átlaga közötti abszolút különbséget a fenti 1. képlettel számoljuk ki:
Δm = │cm - cQCM │ = │14,3-12,9│ μg/kg = 1,4 μg/kg.
Ezután a kombinált (u∆) és a kiterjesztett (U∆) bizonytalanságokat a 2. képlettel kell kiszámítani:
u∆ = √ um2 + uQCM2 = √0,742 + 0,452 μg/kg =0,87 μg/kg =0,87 μg/kg.
U∆ = 2- u∆ = 2 - 0,87 μg/kg = 1,7 μg/kg.
A mért értékek átlaga és a hitelesített érték (∆m = 1,4 μg/kg ) közötti abszolút különbség kisebb, mint a kiterjesztett bizonytalanság (U∆ = 1,7 μg/kg). Ebben a példában nincs jelentős eltérés a mért érték és a hitelesített érték között.
