Pewne niewiadome: Matematyka stojąca za materiałami do kontroli jakości mikotoksyn i jak z niej korzystać
W laboratorium serwisowym są one zazwyczaj analizowane w tych samych warunkach, które są wykorzystywane do analizy próbek klientów. Analiza QCM może generować dane, które laboratoria mogą wykorzystać do sprawdzenia, jak działa nowo opracowana metoda, do rozwiązywania wszelkich problemów z analizą i do generowania wykresów kontroli jakości.
Podczas przeprowadzania walidacji procedur pomiarowych, analitycy porównują wartość wygenerowaną przez każdy pomiar QCM z wartością certyfikowaną podaną w jego certyfikacie. Nieformalnie, niektórzy opisują to porównanie w sposób jakościowy za pomocą stwierdzeń takich jak "zmierzona wartość zgadza się z certyfikowaną wartością materiału kontroli jakości". Podejście ilościowe może jednak porównać te dwie wartości matematycznie, wykluczając w ten sposób stronniczość i zapewniając narzędzie do śledzenia wyników w czasie.
W tym artykule Martina Bellasio poprowadzi Państwa przez podstawy obliczania niepewności pomiaru i sposobu jej ilościowego określania w QCM.
Dlaczego w pomiarach niepewności w QCM preferowane jest podejście ilościowe?
Podejście ilościowe uwzględnia wartość zmierzoną w praktycznym zastosowaniu, wartość certyfikowaną przez producenta QCM oraz ich niepewności. Proszę najpierw pokrótce omówić koncepcję niepewności pomiaru i dlaczego ważne jest, aby wziąć ją pod uwagę.
Wszystkie pomiary są obarczone niepewnością: żaden pomiar nie jest dokładny. Dlatego też niepewność jest kluczowym czynnikiem w interpretacji danych naukowych, ponieważ dostarcza nam informacji o tym, jak dokładna jest przypisana wartość. Określając niepewność związaną z wartością, można przekazać pełniejszy obraz wyników, dzięki czemu stają się one bardziej użyteczne. "ISO Guide to the Expression of Uncertainty in Measurement (GUM)" i przewodnik Eurachem/CITAC "Quantifying Uncertainty in Analytical Measurement" są powszechnie używanymi tekstami referencyjnymi do wyrażania niepewności.
Jak wspomniano wcześniej, porównanie zmierzonych wartości z certyfikowaną wartością materiału kontroli jakości wymaga obliczenia różnicy między tymi dwiema wartościami i tak zwanej niepewności rozszerzonej. W kolejnych akapitach dowiemy się, jak obliczyć te wartości i jak zastosować je w praktycznym przykładzie.
Opublikowano:
Mikotoksyna
Ten artykuł został opublikowany w Spot On #12
Są Państwo ciekawi, co Spot On ma do zaoferowania?
Proszę przeczytać teraz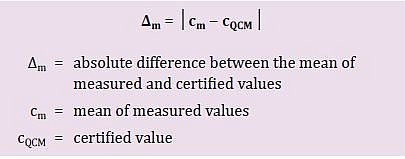
Jak określić stopień, w jakim zmierzona wartość odbiega od wartości certyfikowanej?
Krok 1: Proszę określić różnicę między wartością certyfikowaną a średnią zmierzonych wartości (∆m).
W tym kroku obliczamy bezwzględną różnicę (oznaczoną symbolem ∆m) między wartością certyfikowaną a średnią zmierzonych wartości (wzór 1). Przyjmujemy tutaj średnią zmierzonych wartości, ponieważ każda próbka powinna być mierzona więcej niż jeden raz, aby zagwarantować dokładność wyniku.
Krok 2: Proszę obliczyć łączną niepewność (u∆).
Teraz obliczamy łączną niepewność (u∆) (wzór 2). Aby to zrobić, poszczególne niepewności (patrz poniżej) wartości certyfikowanej i wartości zmierzonych muszą być już znane (patrz ramka "Znajdowanie poszczególnych niepewności"). Wzór 2 przedstawia dokładne operacje matematyczne.
Krok 3: Proszę obliczyć niepewność rozszerzoną (U∆).
Tutaj mnożymy połączoną niepewność przez współczynnik rozszerzenia, zwykle równy 2.
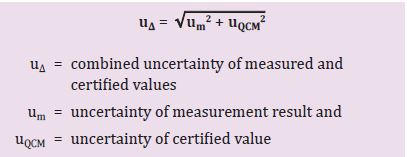
Krok 4: Proszę porównać różnicę między wartością certyfikowaną a wartościami zmierzonymi (∆m) z niepewnością rozszerzoną (U∆).
Bezwzględna różnica między średnią zmierzonych wartości a wartością certyfikowaną (∆m) oraz niepewność rozszerzona (U∆) to dwa główne parametry określające, czy zmierzona wartość znacznie odbiega od wartości certyfikowanej. Definiujemy "znaczącą różnicę" w następujący sposób: jeśli Δm jest mniejsze lub równe U∆, wówczas nie ma znaczącej różnicy między wynikiem pomiaru a wartością certyfikowaną.
Porównanie bezwzględnej różnicy między średnią zmierzonych wartości a wartością certyfikowaną z niepewnością rozszerzoną pozwala na matematyczne podejście do porównywania dwóch wartości i zapewnia zgodność laboratoriów z Przewodnikiem ISO 98-3:2008 (ISO Guide to the Expression of Uncertainty in Measurement, GUM).
Chociaż koncepcja niepewności pomiaru może być nieco trudna do zrozumienia na pierwszy rzut oka, może służyć jako określenie stopnia precyzji procedury pomiarowej w stosunku do innych. Ilościowe określenie tej niepewności znacznie przyczynia się do zapewnienia, że możemy polegać na naszych metodach i uzyskiwać wyniki, które są bardziej obiektywne i mniej zależne od stwierdzeń jakościowych: zamiast na przykład twierdzić, że "zmierzona wartość zgadza się z wartością certyfikowaną", obliczenie niepewności pozwala nam wykreślić i udokumentować odchylenia z większą i bardziej praktyczną precyzją. Dzięki materiałom do kontroli jakości laboratoria dysponują potężnym narzędziem, które może pomóc im w ciągłym doskonaleniu metod.
Poniżej znajduje się przykład, który pomoże wyjaśnić te zasady.
Uwaga: Znaczna część tego tekstu została zaadaptowana z noty aplikacyjnej ERM "Porównanie wyniku pomiaru z wartością certyfikowaną" autorstwa Thomasa Linsingera.
Przykład
QCM ma przypisaną wartość 12,9 μg/kg aflatoksyny, z szacowaną niepewnością rozszerzoną U ± 0,9 μg/kg i współczynnikiem rozszerzenia k = 2. UQCM, niepewność wartości certyfikowanej, można obliczyć dzieląc UQCM przez współczynnik rozszerzenia, dlatego uQCM = 0,9/2 μg/kg= 0,45 μg/kg.
Przeprowadzono 12 pomiarów laboratoryjnych, uzyskując średnią 14,3 ± 1,8 μg/kg. Niepewność zmierzonych wartości (um) w tym przypadku zostanie oszacowana przy użyciu odchylenia standardowego. Odchylenie standardowe jest dzielone przez pierwiastek kwadratowy z liczby pomiarów. um jest w przybliżeniu obliczane jako 1,8/√6 μg/kg = 0,74 μg/kg.
Mając pod ręką zarówno niepewność wartości certyfikowanej, jak i niepewność pomiaru, możemy teraz ocenić, czy istnieje znacząca różnica między wartością zmierzoną a wartością certyfikowaną.
Po pierwsze, bezwzględna różnica między średnią zmierzonych wartości a wartością certyfikowaną jest obliczana za pomocą wzoru 1 z góry:
∆m = │cm - cQCM │ = │14,3-12,9│ μg/kg = 1,4 μg/kg
Następnie, połączone (u∆) i rozszerzone (U∆) niepewności są obliczane za pomocą wzoru 2:
u∆ = √ um2 + uQCM2 = √0,742 + 0,452 μg/kg =0,87 μg/kg
U∆ = 2- u∆ = 2 - 0,87 μg/kg = 1,7 μg/kg
Bezwzględna różnica między średnią zmierzonych wartości a wartością certyfikowaną (∆m = 1,4 μg/kg) jest mniejsza niż niepewność rozszerzona (U∆ = 1,7 μg/kg). W tym przykładzie nie ma znaczącego odchylenia między wartością zmierzoną a wartością certyfikowaną.
